피보나치 수
피보나치 수는 첫째 및 둘째 항이 1이며
그 뒤의 모든 항은 바로 앞 두항의 합인 수열
처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다.
편의상 0번째 항을 0으로 두기도 한다.
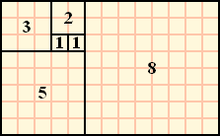
내용 출처 - 위키백과 -
함수를 구현해 보면
자바
public static long getFiboNum(long n) {
if(n == 1 || n == 2) return 1L;
return getFiboNum(n-1) + getFiboNum(n-2);
}
파이썬
def fibo(n):
if n in [1, 2]:
return 1
return fibo(n-1) + fibo(n-2)
수행문이 고작 2~3줄이다.
매우 간단하다. 하지만...
fibo(1) : 1
fibo(2) : 1
fibo(3) : fibo(2) + fibo(1)
= 1 + 1 = 2
fibo(4) : fibo(3) + fibo(2)
= fibo(2) + fibo(1) + fibo(2)
= 1 + 1 + 1 = 3
fibo(5) : fibo(4) + fibo(3)
= fibo(3) + fibo(2) + fibo(2) + fibo(1)
= fibo(2) + fibo(1) + fibo(2) + fibo(2) + fibo(1)
= 1 + 1 + 1 + 1 + 1
= 5
fibo(6) : fibo(5) + fibo(4)
= fibo(4) + fibo(3) + fibo(3) + fibo(2)
= fibo(3) + fibo(2) + fibo(2) + fibo(1) + fibo(2) + fibo(1) + fibo(2)
= fibo(2) + fibo(1) + fibo(2) + fibo(2) + fibo(1) + fibo(2) + fibo(1) + fibo(2)
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
= 8
.
.
.
내가 직접 해보았지만
조금만 수가 늘어나도 기하급수적으로
연산 횟수가 늘어난다;;
컴퓨터가 이러한 연산을 하면
30, 40, 50... 100을 넘어가면
나중에는 컴퓨터를 켜놓고 밥먹고와도
연산중일 것이다.

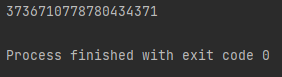
fibo(100) = 354224848179261915075
fib(5) 연산
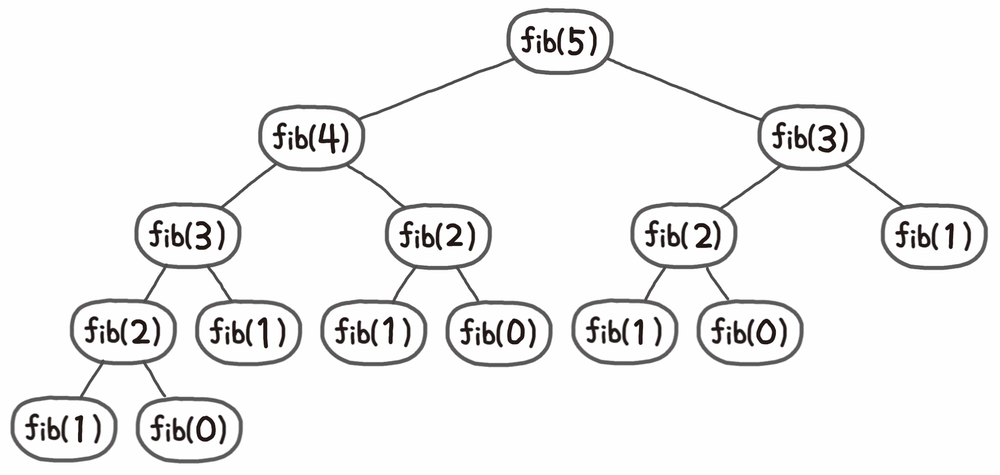
그림을 보면
fib(5)를 구하기 위해
fib(3)은 2번 구하고 있다.
수열이 커질수록 이러한 중복에 대한
연산을 많이 하게 된다.
그럼 당연히 연산속도는 느려질 수밖에 없다.
메모이제이션(memoization)을 활용하면
계산되었던 결과를 저장하여
이전의 연산결과를 바로 불러오면 되므로
시간적으로 많이 줄어든다.
동적 계획법의 핵심이라고 한다.
메모이제이션을 활용하여 자바코드를 짜보았다.
자바는 Map을 이용하여 구현해보았다.
import java.util.HashMap;
import java.util.Map;
public class Main {
static Map<Long, Long> memo = new HashMap<>();
public static void main(String[] args) {
memo.put(1L, 1L);
memo.put(2L, 1L);
System.out.println(getFiboNum(100L));
}
public static long getFiboNum(Long n) {
if(memo.containsKey(n)) return memo.get(n);
memo.put(n, getFiboNum(n-1) + getFiboNum(n-2) );
return memo.get(n);
}
}
메모이제이션을 활용하여 파이썬 코드도 짜보았다.
memo = {1: 1, 2: 1}
def fibo(n) :
if n in memo:
return memo[n]
memo[n] = fibo(n-1) + fibo(n-2)
return memo[n]
print(fibo(100))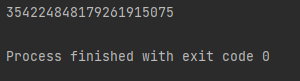
파이썬과 자바로
피보나치 수열을 구현해보았다.
메모이제이션을 이용하면
시간단축이 엄청나게 많이 된다는
것을 알게되었다.
'알고리즘 탐구' 카테고리의 다른 글
| 프로그래머스) (자바) 직사각형 별 찍기 (0) | 2023.04.09 |
|---|---|
| 프로그래머스) (자바)핸드폰 번호 가리기 (0) | 2023.04.07 |
| 백준) (자바)1935 후위 표기식 2 (0) | 2023.04.04 |
| 알고리즘) 유클리드 호제법 (0) | 2023.03.16 |
| 알고리즘) 동적 계획법 (0) | 2023.03.15 |
